lunes, 19 de abril de 2010
ATOMISMO LOGICO por Bertrand Russell
jueves, 8 de abril de 2010
Obra de Kurt Gödel
http://thales.cica.es/rd/Recursos/rd97/Biografias/08-1-b-godel.html
La obra lógica de Gödel hay que relacionarla desde el principio con el programa formalista de Hilbert. Su tesis doctoral fue su famosa prueba de la suficiencia semántica del cálculo lógico de primer orden, y sólo tenía 11 páginas. Dos años antes, Hilbert y Ackermann habían delimitado de un modo claro la lógica de primer orden y presentado un cálculo lógico para ella. Dicho cálculo no era completo sintácticamente en el sentido de que para cada fórmula o bien ella o bien su negación fuera deducible. Esto es así ya que un cálculo lógico solo pretende generar las fórmulas válidas (fórmulas verdaderas bajo cualquier interpretación), y hay muchas fórmulas tales que ni ellas ni su negación son válidas. Lo que si podía plantearse era la cuestión de si el cálculo era semánticamente suficiente, es decir, si permitía deducir todas las fórmulas válidas. Hilbert y Ackermann no habían encontrado respuesta a esta pregunta en 1928, y eso precisamente es lo que hizo Gödel dos años después, dando respuesta positiva: el cálculo lógico de primer orden era lo suficientemente potente como para deducir todas las fórmulas válidas (y sólo estas). Este resultado marcó un jalón en la historia de la Lógica Moderna y supuso un espaldarazo prometedor para el programa formalista de Hilbert.
El resultado más revolucionario de la Lógica del siglo XX, por el que Kurt Gödel es especialmente famoso, es el teorema de incompletitud, publicado en 1931. Este teorema es más fácil de entender si nos aproximamos a él indirectamente. Con este fin, presentaremos un rompecabezas lógico y algunos términos clave antes de pasar a la discusión del teorema propiamente dicha.
Hay una antigua afirmación paradójica, llamada paradoja del mentiroso, que puede ayudarnos a ilustrar el tema: "Esta afirmación es falsa." Pasemos a analizar tal afirmación. Si esta es verdadera, esto significa que la afirmación es falsa, lo cual contradice nuestra primera hipótesis. Por otra parte, si la afirmación es falsa, la afirmación debe de ser verdadera, lo cual nos lleva de nuevo a una contradicción. Una versión aun más simple de esta paradoja (como señaló Lewis Carrol) es la afirmación siguiente: "Yo estoy mintiendo." En estas afirmaciones se presenta el fenómeno llamado bucle extraño. Cualquier suposición inicial que se haga conduce a una refutación de ésta. Muchas de las ilusiones ópticas del arte de M. C. Escher están basadas en este concepto.
Otro término importante es el de isomorfismo. Entenderemos aquí un isomorfismo como una conexión entre un nivel del entendimiento y otro. El isomorfismo más común es el que se da entre el lenguaje y la mente. Estas palabras que usted está leyendo son combinaciones de líneas que tienen un significado atribuido. Ellas no significan nada por sí mismas, son meras conexiones con conceptos que están en nuestras mentes. Este es un ejemplo difícil, ya que estamos tan acostumbrados a hablar y escribir que olvidamos que las letras y las palabras no son la verdadera comunicación. Otro ejemplo es el sistema de numeración romana. Sabemos como expresar números arábigos (los cuales son isomorfos a dedos, rocas, etc.) en el sistema romano, pero ello es algo peliagudo. Estamos enterados del isomorfismo entre estos dos sistemas tipográficos desde el momento en el que necesitamos trasladarnos del uno al otro constantemente.
El último término a considerar es el de sistema formal. Este término parece bastante fácil, pero su propia naturaleza hace necesario definirlo explícitamente. Llamaremos sistema formal a un sistema tipográfico que sea isomorfo a la teoría de números. Esto es comparable a tomar las expresiones de lenguaje natural de las demostraciones geométricas y sustituirlas por símbolos que tengan el mismo significado. Se hace esto para evitar la ambigüedad y fomentar la precisión. El punto a tener en cuenta a la hora de trabajar con sistemas formales es que no podemos usar el sentido común o, en general, cualquier argumento ajeno al sistema. El Formalismo es un movimiento, en la Lógica y en las Matemáticas, impulsado por Hilbert en los años 20. Hilbert inventó un artificial lenguaje de la lógica y comenzó a trasladar las afirmaciones de la teoría de números dentro de él. Su propósito era construir sistemas formales completos para las principales teorías de la matemática clásica. Completos en el sentido de que cualquier afirmación puede o bien ser demostrada o bien ser demostrada su negación. El programa de Hilbert también requería que se demostrara la consistencia de dichos sistemas formales.
El teorema de incompletitud de Gödel es bastante sencillo de entender una vez hemos introducido la paradoja del mentiroso (citada más arriba). Gödel hizo manipulaciones para trasladar el lenguaje natural del mentiroso al lenguaje de las matemáticas. Lo que probó es comparable (isomorfo) a la afirmación "Este teorema no tiene demostración". ¡Lo sorprendente es que él probó el teorema! Diseñó su propio lenguaje lógico para esto. En definitiva, descubrió que existían afirmaciones verdaderas que no podían ser probadas dentro del sistema.
Gödel probó que todo sistema formal que contuviera a la aritmética elemental (un ejemplo de este sistema serían las Matemáticas como un todo) es incompleto. Además, por el camino encontró que la consistencia de dichos sistemas era imposible de probar. Esto no significó el fin del Formalismo, pero supuso un duro golpe para este.
También hizo grandes contribuciones a la Teoría de Conjuntos, como la demostración de la consistencia relativa del axioma de elección y de la hipótesis del continuo respecto del resto de los axiomas. Además, hizo importantes contribuciones al estudio del problema de la decisión, definió por primera vez las funciones recursivas, probó la consistencia de la lógica y aritmética clásica respecto de la intuicionista, se ocupó de la cosmología relativista y encontró soluciones sorprendentes a las ecuaciones del campo gravitatorio de la relatividad general.
miércoles, 25 de noviembre de 2009
La intuición matemática: instinto básico de los primates
En una revisión publicada en Trends in Cognitive Sciences [1], Jessica Cantlon, actualmente en la Universidad de Rochester, y sus colaboradores, analizan las últimas investigaciones que apuntan a que la capacidad para las matemáticas es innata en los primates, incluido el hombre.
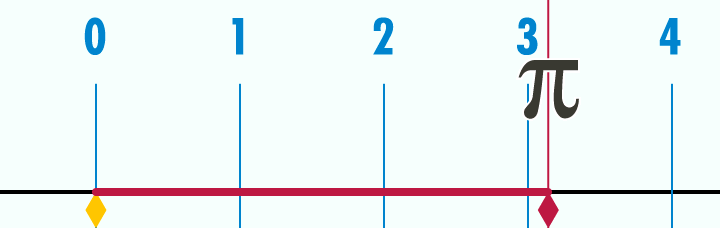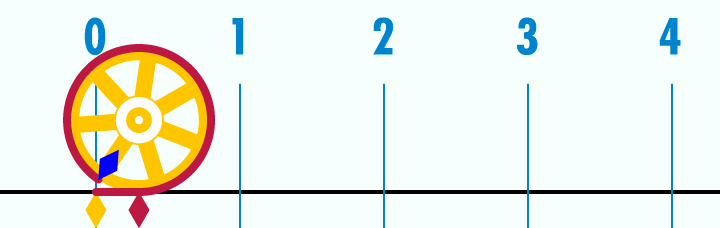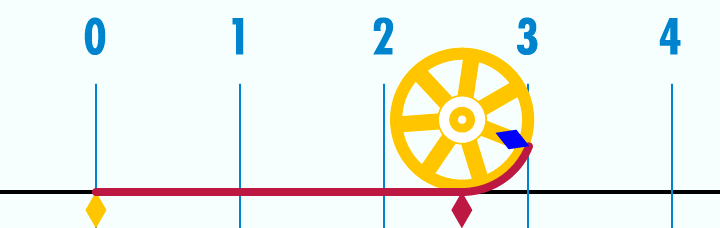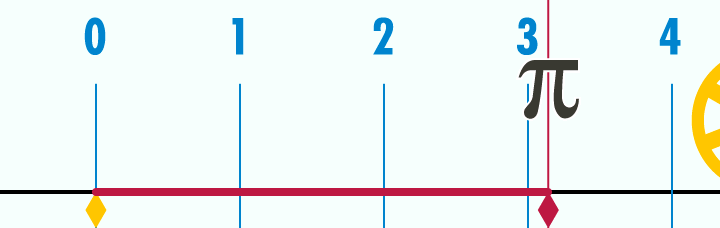
Tradicionalmente se ha pensado que aprendemos a usar los números de la misma forma que aprendemos a conducir un coche. Desde este punto de vista, los números son una especie de tecnología, una invención del hombre a la que nuestro cerebro multiuso se puede adaptar. La historia parece apoyar esta idea. La prueba más antigua del uso de números tiene más de 30.000 años: huesos y cuernos con muescas que son consideradas por los arqueólogos como marcas de cuentas. Los usos más complejos de los números aparecieron mucho más tarde, coincidiendo con la aparición de otras tecnologías. En Mesopotamia apareció la aritmética básica hace alrededor de 5.000 años. El cero no se encuentra hasta el año 876 de la era común. Los estudiosos árabes establecieron los rudimentos del álgebra en el siglo IX; el cálculo no apareció completo hasta finales del XVII.
A pesar de la aparición tardía de las matemáticas superiores, hay cada vez más pruebas de que los números no son realmente una invención reciente. Nuestra especie parece tener una habilidad innata para las matemáticas, una habilidad que nuestros ancestros de hace 30 millones de años ya habrían tenido.
Si la habilidad para las matemáticas fuese realmente innata debería poder detectarse de alguna manera en los niños pequeños. Esto es precisamente lo que hizo el equipo encabezado por Veronique Izard (Harvard; EE.UU.) en un estudio con recién nacidos [2]. Izard y sus colegas reprodujeron sonidos de arrullo a los bebés, con un número variable de sonidos en cada ensayo. A los bebés se les mostraba después un conjunto de formas en una pantalla de ordenador, y los científicos medían cuanto tiempo la miraban (la cantidad de tiempo que un bebé pasa mirando un objeto es proporcional a su interés). Los recién nacidos miraban consistentemente más tiempo a la pantalla cuando el número de formas coincidía con el número de sonidos que acababan de escuchar. Este estudio de Izard et ál. sugiere que los recién nacidos tienen una comprensión básica de los números. No sólo eso, esta comprensión es abstracta: pueden transferirla entre los sentidos, de sonidos a imágenes.
La intuición matemática se desarrolla conforme crecemos, pero es difícil seguir su desarrollo porque conforme los niños crecen se basan tanto en sus habilidades innatas como en lo que aprenden. Por ello los investigadores han tenido que ingeniar métodos para forzar a la gente a que se base sólo en la intuición. Elizabeth Brannon (Duke; EE.UU.), coautora de la revisión, en colaboración con Cantlon, realizó un experimento [3] en el que sujetos adultos veían un conjunto de puntos en una pantalla de ordenador durante medio segundo, seguido por otro segundo conjunto. Después de una pausa, los participantes podían ver dos conjuntos de puntos uno al lado del otro. A partir de ese momento disponían de poco más de un segundo para señalar el conjunto suma de los dos anteriores.
A los participantes les suele ir muy bien en ese tipo de tests, lo que les provoca una sensación extraña: saben que tienen razón, pero no saben cómo obtuvieron la respuesta. Incluso en los niños pequeños que todavía no saben contar, según estudios similares, el cerebro procesa los números automáticamente. Desde la infancia hasta la ancianidad, la intuición matemática sigue dos reglas consistentemente. Una es que la gente obtiene mejores resultados cuando los números son pequeños que cuando son grandes. La otra es que se obtienen mejores resultados cuando la diferencia entre los números es mayor. En otras palabras, es más probable que la gente distinga entre 2 y 4 que entre 6 y 8, aunque la diferencia sea la misma. Conforme vamos acumulando años, nuestra intuición se hace más precisa. Otros experimentos han demostrado que un bebé de 6 meses puede distinguir con seguridad entre números cuya razón sea 2 (como 8 y 4). A los 9 meses la razón cae a 1,5 (12 y 8, por ejemplo). Y cuando es adulto la razón es sólo 0,1. El hecho de que las dos reglas se mantengan en todos los casos sugiere que usamos el mismo algoritmo mental a lo largo de nuestras vidas.
Los escáneres cerebrales que usan imágenes por resonancia magnética (MRI, por sus siglas en inglés) y tomografía por emisión de positrones (PET, por sus siglas en inglés) están arrojando algo de luz en cómo nuestros cerebros llevan a cabo este algoritmo. Los neurocientíficos han encontrado que, cuando nuestro cerebro realiza problemas de intuición matemática, un conjunto de neuronas cerca de la parte más alta del cerebro, que rodea el surco intraparietal, se activa consistentemente. Y cuando nos enfrentamos a problemas más difíciles, cuando los números son mayores o más próximos, esta región se activa aún más.
Los investigadores sospechan que la intuición matemática que estas neuronas ayudan a producir constituye el cimiento sobre el que se construye el resto de las matemáticas más sofisticadas. Justin Halberda (Johns Hopkins; EE.UU.) y sus colegas realizaron un estudio [4] sobre intuición matemática con un grupo de adolescentes de 14 años. Algunos mostraron mayor intuición que otros. Un análisis de los resultados escolares demostró que los que demostraban mejor intuición habían obtenido mejores resultados en los exámenes estandarizados de matemáticas desde preescolar.
El hecho de que los niños posean una intuición matemática mucho antes de que empiecen el colegio implica que nuestros ancestros también la tenían. De hecho, investigaciones recientes revelan que nuestros ancestros la tenían incluso antes de que pudiesen andar erguidos. Se ha encontrado que muchos primates, incluyendo los monos rhesus, pueden resolver algunos de los problemas matemáticos que nosotros podemos [3]. Dado que los monos y los humanos divergieron hace 30 millones de años, la intuición matemática es al menos así de antigua.
La intuición matemática como instinto básico de los primates (2ª parte y última).
Dando pruebas de la herencia compartida, Cantlon y Brannon fueron capaces de demostrar que los monos suman por intuición de la misma forma que lo hacen los humanos [3, de la 1ª parte]. La intuición de los animales es casi tan buena como la nuestra, y sigue las mismas reglas, conforme la razón entre los números se hace mayor, es más probable que los monos escojan el resultado correcto. Y cuando los monos usan su intuición matemática se basan en la misma región alrededor del surco intraparietal en la que nos apoyamos nosotros.
Los monos pueden aprender también a reconocer las grafías de los números, una habilidad que los niños desarrollan alrededor de los 5 años. Con objeto de hacer la conexión entre la grafía 2 y un par de objetos se activa una región del cerebro de los niños llamada córtex prefrontal dorsolateral. Esta región es como una herrería para forjar asociaciones entre signos y conceptos. Una vez que la asociación se ha creado los niños reconocen las grafías de los números rápidamente, sin que se vuelva a activar el córtex prefrontal dorsolateral.
Los monos pueden aprender, con suficiente entrenamiento a señalar un 4 si ven cuatro puntos en una pantalla. Andreas Nieder (Tubinga; Alemania) y sus colegas han descubierto [5] que, al igual que los niños, los monos usan el córtex prefrontal dorsolateral para hacer esas asociaciones. Incluso han encontrado neuronas individuales en esta región que se activan fuertemente tanto ante la presencia de cuatro puntos como de la grafía 4.
Pero, ¿comprende realmente un mono lo que la grafía 4 significa? Para averiguarlo, Nieder y su antigua alumna Ilka Diester entrenaron monos para un nuevo experimento [6]. Los monos aprendieron a pulsar una palanca, tras lo cual veían un número seguido de otro. Si lo números coincidían, los monos podían soltar la palanca para conseguir un chorrito de zumo. Si los números no coincidían, los monos tenían que mantener la palanca pulsada hasta que aparecía un nuevo número, que siempre coincidía.
Los monos aprendieron ha soltar la palanca cuando los números coincidían y a mantenerla pulsada para los números que no casaban. Si hubiesen tenido éxito simplemente fijándose en la forma, cabría haber esperado que confundiesen grafías similares, como 1 y 4, ambas hechas a partir de líneas rectas. Pero Diester y Nieder pudieron comprobar que los monos se equivocaban de otra manera. Era más probable que los monos se confundiesen cuando aparecían grafías que representaban valores numéricos próximos: el recto 1 con el curvilíneo 2, por ejemplo. No sólo eso, los monos empleaban más tiempo en soltar la palanca si la coincidencia era entre números grandes que si era entre pequeños, otra señal de que los monos estaban respondiendo a la cantidad, no a la forma.
Para los neurocientíficos, estos estudios plantean una cuestión importante. Si los monos tienen unos fundamentos tan sólidos para los números, ¿por qué no pueden realizar matemáticas superiores? Encontrar una respuesta nos ayudaría a comprender qué es lo que nos permite a los humanos ser mucho mejores con los números que el resto de animales. Tanto Nieder como Cantlon han especulado con la idea de que la diferencia está en nuestra capacidad para comprender símbolos, lo que nos permitiría transformar nuestra intuición de los números en una comprensión precisa. Cuando decimos “2” queremos decir una cantidad exacta, no “probablemente 2 pero puede que 1 ó 3”. Podemos entonces aprender reglas para manejar números exactos rápidamente, para después generalizar estas reglas, dando paso así a principios matemáticos generales. Los otros primates, careciendo de cerebros simbólicos como los nuestros, necesitan miles de intentos para aprender una nueva regla.
Los recientes estudios con monos y niños arrojan nueva luz sobre los huesos con muescas de los que hablábamos al principio (1ª parte). Los primeros números registrados coinciden con la aparición de muchas otras expresiones de pensamiento abstracto, desde flautas de hueso a grabados o figuras de mujeres (venus). Antes de todo esto, los humanos habrían concebido los números de la forma en que los monos (y los niños pequeños) todavía lo hacen hoy. Pero una vez que nuestros antepasados comenzaron a unir su instinto natural para los números con una nueva capacidad para comprender símbolos, todo cambió. Las matemáticas llegaron a ser el idioma de las ideas, de las mediciones, y de las posibilidades de la ingeniería. El resto de la civilización fue sólo una cuestión de deducción.
Referencias:
[5] Nieder, A. (2009). Prefrontal cortex and the evolution of symbolic reference Current Opinion in Neurobiology, 19 (1), 99-108 DOI: 10.1016/j.conb.2009.04.008
viernes, 25 de septiembre de 2009
¿que es la ciencia?
No siempre los modelos científicos son una fiel imagen de la realidad. Los átomos y las moléculas que componen el aire que respiramos, por ejemplo, se pueden describir en términos de un modelo en el que imaginamos cada partícula como si fuera una pequeña esfera perfectamente elástica, con todas las pequeñas esferas rebotando unas contra otras y contra las paredes del recipiente que las contiene.
Esa es la imagen mental, pero es sólo la mitad del modelo; lo que lo hace modelo científico es describir el modo como se mueven las esferas y rebotan unas contra otras mediante un grupo de leyes físicas, escritas en términos de ecuaciones matemáticas. En este caso, éstas son esencialmente las leyes del movimiento descubiertas por Newton hace más de trescientos años. Utilizando estas leyes matemáticas es posible predecir, por ejemplo, que le pasará a la presión ejercida por un gas si se aplasta hasta la mitad de su volumen inicial. Si hacemos el experimento, y, el resultado que se obtiene encaja con la predicción del modelo, este será un buen modelo.
De hecho, todos los modelos científicos tienen aplicabilidad limitada. Ninguno de ellos es “la verdad “. Cuando un científico afirma, por ejemplo, que el núcleo de un átomo está compuesto por partículas denominadas protones y neutrones, lo que en realidad debería decir es que el núcleo de un átomo se comporta, bajo determinadas circunstancias, como si estuviera formado de protones y neutrones. Los mejores científicos toman el “como sí “, pero entienden que sus modelos son, efectivamente, sólo modelos; científicos menores a menudo olvidan esta diferencia crucial.
Los científicos menores, y muchos no-científicos, tienen otra idea equivocada. A menudo piensan que el papel de los científicos hoy en día es llevar a cabo experimentos que probarán la exactitud de sus modelos con una precisión cada vez mayor (hacia posiciones con más y más decimales). ¡En absoluto! La razón para llevar a cabo experimentos que demuestren predicciones previas no comprobadas es descubrir dónde fallan los modelos. Encontrar defectos en sus modelos es la esperanza abrigada por los mejores científicos, porque esos defectos destacarán los lugares donde necesitamos una nueva comprensión, con modelos mejores, para progresar.
El arquetípico ejemplo de esto es la gravedad. La ley de la gravedad de Isaac Newton se consideró la pieza clave de la física durante más de doscientos años, desde la década de 1680 hasta comienzos del siglo XX. Pero había unas pocas, aparentemente insignificantes, cosas que el modelo newtoniano no podía explicar o predecir, referente a la órbita del planeta mercurio y al modo como la luz se curva cuando pasa cerca del Sol. El modelo de gravedad de Albert Einstein, basado en su teoría general explica lo mismo que el modelo de Newton pero también explica esos detalles sutiles de órbitas planetarias y curvatura de la luz. En ese sentido, es un modelo mejor que el anterior, y hace predicciones correctas (en particular, sobre el Universo en general) que el viejo modelo no hace. Pero el modelo de Newton todavía es todo lo que se necesita si se está calculando el vuelo de una sonda espacial desde
viernes, 18 de septiembre de 2009
1854: La geometría curva entre Newton y Einstein
Para distancias físicas pequeñas la geometría euclidiana sirve.
Newton elaboró sus leyes con base en la geometría euclidiana (y con los conceptos de espacio y tiempo absolutos e independientes).
Pero en el espacio esto ya no es así. Geometrías no euclidianas son las que sirven para explicar fenómenos estelares.
Los rayos de luz se toman como las líneas rectas de la geometría espacial. Pero los rayos de luz se distorsionan (se ``curvan'') por la acción gravitatoria de las masas planetarias.
El Sol, la Tierra, la Luna, Júpiter y otros astros distorsionan los rayos de luz.
La masa planetaria distorsiona los rayos de luz
La geometría curva de Riemann
por Emilio Silvera - Recuerdo aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.
Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria, arruinó su vida en la tuberculosis y en la miseria mas abyecta .
Nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un humilde predicador luterano que se esforzó inutilmente para alimentar a su pobre familia a la cual, la miseria mas una delicada salud que llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.
A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del hostil mundo exterior.
Para salvar a su familia, Riemann se propuso hacerse estudiante de teología y obtener un puesto remunerado como pastor. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a verdad de las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por manifestaciones y levantamientos, fue reclutado para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
Tambien frente a tan terrible en aquel ambiente, se refugio en la verdad de las matematicas, el problema en que se refugio Riemann, (y que si podia resolver) fue el desastre que suponía el espacio “plano” tal como lo sostiene la geometría euclidiana.
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”, para rematar en el año 150 d. C. Ptolomeo de Alejandría con una "demostración” de que la cuarta dimensión es imposible.
En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a quizás las dos mayores ideas de la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
Riemann hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.
Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a*a + b*b = c*c. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.
Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.